深度基础知识系列(一) 优化器介绍

一、梯度下降法(Gradient Descent)

    微积分中，对多元函数的参数求$ \theta$偏导数，把求得的各个参数的导数以向量的形式写出来就是梯度。梯度就是函数变化最快的地方。梯度下降是迭代法的一种，在求解机器学习算法的模型参数 $ \theta$ 时，即无约束问题时，梯度下降是最常采用的方法之一。顾名思义，梯度下降法的计算过程就是沿梯度下降的方向求解极小值，也可以沿梯度上升方向求解最大值。 假设模型参数为$ \theta$，损失函数为$ J(\theta)$ ，损失函数$ J(\theta)$关于参数$ \theta$的偏导数，也就是梯度为 $ \nabla_{\theta}J(\theta)$ ，学习率为 $ \alpha$，则使用梯度下降法更新参数为：

$$\theta_{t+1} = \theta_t - \alpha ·\nabla_{\theta}J(\theta)$$

    梯度下降法目前主要分为三种方法,区别在于每次参数更新时计算的样本数据量不同：批量梯度下降法(BGD, Batch Gradient Descent)，随机梯度下降法(SGD, Stochastic Gradient Descent)及小批量梯度下降法(Mini-batch Gradient Descent)。

1、批量梯度下降法(BGD, Batch Gradient Descent)

    假设训练样本总数为n，样本为 $ {(x^1,y^1) ···(x^n,y^n)}$ ，模型参数为$ \theta$，损失函数为$ J(\theta)$ ，在第i对样本 $ (x^i,y^i) $上损失函数关于参数的梯度为 $ \nabla_{\theta}J(\theta,x^i,y^i)$ , 学习率为 $ \alpha$，则使用BGD更新参数为：

$$\theta_{t+1} = \theta_t - \alpha_t ·\sum_{i=1}^n\nabla_{\theta}J_i(\theta,x^i,y^i)$$

特点：

1、每进行一次参数更新，需要计算整个数据样本集，因此导致批量梯度下降法的速度会比较慢，尤其是数据集非常大的情况下，收敛速度就会非常慢

2、由于每次的下降方向为总体平均梯度，它得到的会是一个全局最优解。

2、随机梯度下降法(SGD, Stochastic Gradient Descent)

    随机梯度下降法，不像BGD每一次参数更新，需要计算整个数据样本集的梯度，而是每次参数更新时，仅仅选取一个样本$ (x^i,y^i) $计算其梯度，参数更新公式为：

$$\theta_{t+1} = \theta_t - \alpha_t ·\nabla_{\theta}J_i(\theta,x^i,y^i)$$

特点：

1、可以看到BGD和SGD是两个极端，SGD由于每次参数更新仅仅需要计算一个样本的梯度，训练速度很快，即使在样本量很大的情况下，可能只需要其中一部分样本就能迭代到最优解

2、由于每次迭代并不是都向着整体最优化方向，导致梯度下降的波动非常大，更容易从一个局部最优跳到另一个局部最优，准确度下降。

3、小批量梯度下降法(Mini-batch Gradient Descent)

    小批量梯度下降法就是结合BGD和SGD的折中，对于含有n个训练样本的数据集，每次参数更新，选择一个大小为m (m<n)的mini-batch数据样本计算其梯度，其参数更新公式如下：

$$\theta_{t+1} = \theta_t - \alpha ·\sum_{i=x}^{i=x+m-1}\nabla_{\theta}J_i(\theta,x^i,y^i)$$

    超参数建议值：$ m\in[50,256]$

特点:

1、小批量梯度下降法即保证了训练的速度，又能保证最后收敛的准确率，目前的SGD默认是小批量梯度下降算法。

PS：SGD的缺点

1、选择合适的learning rate比较困难 ，学习率太低会收敛缓慢，学习率过高会使收敛时的波动过大

2、所有参数都是用同样的learning rate

3、SGD容易收敛到局部最优，并且在某些情况下可能被困在鞍点

二、动量优化法

    动量优化方法引入物理学中的动量思想，加速梯度下降，有Momentum和Nesterov两种算法。当我们将一个小球从山上滚下来，没有阻力时，它的动量会越来越大，但是如果遇到了阻力，速度就会变小，动量优化法就是借鉴此思想，使得梯度方向在不变的维度上，参数更新变快，梯度有所改变时，更新参数变慢，这样就能够加快收敛并且减少动荡。

1、Momentum

    momentum算法思想：参数更新时在一定程度上保留之前更新的方向，同时又利用当前batch的梯度微调最终的更新方向，简言之就是通过积累之前的动量来加速当前的梯度。假设$ m_t$表示t时刻的动量，$ \mu$ 表示动量因子，通常取值0.9或者近似值，在SGD的基础上增加动量，则参数更新公式如下：

$$m_{t+1} = \mu ·m_t + \alpha·\nabla_{\theta}J(\theta) \\ \theta_{t+1} = \theta_t - m_{t+1}$$

    超参数建议值：$ \mu=0.9$

特点：

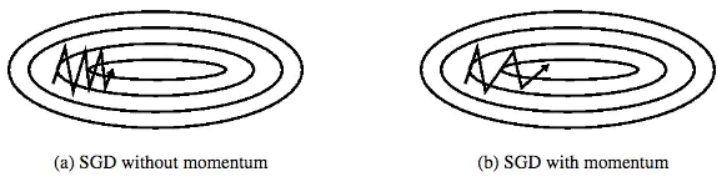
1、momentum能够降低参数更新速度，从而减少震荡。

2、在梯度方向相同时，momentum可以加速参数更新， 从而加速收敛。

2、NAG（Nesterov accelerated gradient）

    但是，让“球”无脑地沿着斜坡向下滚并不总能得到让人满意的解。我们更希望有这样的一个小球，它能够对下一步怎么滚有个基本的“主见“，在滚过斜坡遇到上坡时，能够减速，防止越过最优解。NAG则在动量法的基础上引入了”预测“的功能。在动量法中，我们用$ \mu·m_t$更新参数$ \theta$，及先让小球按照惯性前进，计算出该处的梯度，便可以对其进行一个初步的预估。

$$m_{t+1} = \mu ·m_t + \alpha·\nabla_{\theta}J(\theta-\mu·m_t) \\ \theta_{t+1} = \theta_t - m_{t+1}$$

    当动量法第一次计算当前梯度时（短蓝线），并在累积梯度方向上进行了一大步参数更新（长蓝线）；NAG是首先在之前的梯度方向上走了一大步（棕色线），然后在此位置上评估一下梯度，最后做出一个相对正确的参数更新（绿线）。这种“先知”更新方法可以避免走过头而逃离了最优解——这在RNN相关的各种任务中收益甚好。

    超参数建议值：$ \mu=0.9$

特点：

1、该方法用到了loss函数的二姐信息，比momentum收敛速度更快，波动更小

三、自适应学习率优化算法

    在机器学习中，学习率是一个非常重要的超参数，但是学习率是非常难确定的，虽然可以通过多次训练来确定合适的学习率，但是一般也不太确定多少次训练能够得到最优的学习率，玄学事件，对人为的经验要求比较高，所以是否存在一些策略自适应地调节学习率的大小，从而提高训练速度。 目前的自适应学习率优化算法主要有：AdaGrad算法，RMSProp算法，Adam算法以及AdaDelta算法。

1、AdaGrad

    AdaGrad可以自适应的调节学习率：对于很少更新的参数采用较大的学习率，对于频繁更新的参数采取更小的学习率——非常适合处理稀疏的数据。谷歌的Dean等人发现，在使用它训练大规模神经网络时，Adagrad很大程度上提升了SGD的鲁棒性。同时，Penningto等人用它来训练GloVe词嵌入模型，因为低频词相对高频词需要更大的学习步长。

$$g_{t,i} = \nabla J(\theta_{e,i}) \\ G_{t,i} = G_{t-1,i} + g_{t,i}^2 \\ \theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{G+\epsilon}} ·g_{t,i} \\ \epsilon 是一个小的常数，用来防止分母未0，一般取10^{-6}$$

    超参数建议值：$ \eta=0.01$

特点:

1、Adagrad的好处在于，它避开了人工调参学习率的问题，绝大部分开源库实现只需要在开始的时候设置η=0.01即可。

2、主要缺点在于它累积了历史梯度作为分母：因为每一个新梯度平方后都是非负值，在训练过程中，分母会越来越大，导致学习率整体会减小直至最后无限小——意味着算法不再能够学习到新的知识。

2、RMSprop

    RMSprop是Hinton在他的Coursera课程上提出的（未公布）的自适应学习率的梯度优化方法。它和Adadelta关注和解决的问题是一样的——学习率的单调递减问题。

$$g_{t} = \nabla J(\theta_{e}) \\ E[g^2]_t = \rho E[g^2]_{t-1} +(1-\rho) g_{t}^2 \\ \Delta \theta_t = \frac{\eta}{\sqrt{E[g^2]_t+\epsilon}} ·g_{t} \\ \theta_{t+1} = \theta_{t} - \Delta \theta_t$$

    超参数建议值：$ \rho=0.9，\eta=0.001$

特点：

1、其实RMSprop依然依赖于全局学习率 [公式]
2、RMSprop算是Adagrad的一种发展，和Adadelta的变体，效果趋于二者之间
3、适合处理非平稳目标——对于RNN效果很好

3、Adadelta

    Adadelta是AdaGrad的一种拓展形式——Adadelta仅考虑了一个历史时间窗口下的累积梯度（在实现上并非存储历史梯度，而是借助衰减因子），避免了Adagrad中学习率总是单调递减的问题。

$$E[g^2]_t = \rho E[g^2]_{t-1} +(1-\rho) g_{t}^2 \\ 初始化 \Delta \theta_t = \frac{\eta}{\sqrt{E[g^2]_t+\epsilon}} ·g_{t} \\ E[\Delta \theta^2]_t = \rho E[\Delta \theta^2]_{t-1} +(1-\rho) \Delta \theta_t^2 \\ 记\ \ RMS[g]_t = \sqrt{E[g^2]_t+\epsilon} \\ 记\ \ RMS[\Delta \theta]_t = \sqrt{E[\Delta \theta^2]_t+\epsilon} \\ \Delta \theta_t = \frac{RMS[\Delta \theta]_t}{RMS[g]_t} ·g_t \\ \theta_{t+1} = \theta_{t} - \Delta \theta_t$$

    超参数建议值：$ \rho=0.9$

特点：

1、训练初中期，加速效果不错，很快。

2、训练后期，反复在局部最小值附近抖动。

4、Adam: Adaptive Moment Estimation

    这个算法是另一种计算每个参数的自适应学习率的方法。相当于 RMSprop + Momentum

    除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 $ v_t$ 的指数衰减平均值 ，也像 momentum 一样保持了过去梯度 $ m_t​$ 的指数衰减平均值

$$初始化m,v=0 \\ m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t \\ v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\ 对m、v做偏差矫正(初始化为0带来的向0偏置的问题) \\ \hat{m}_t = \frac{m_t}{1-\beta_1} \\ \hat{v}_t = \frac{v_t}{1-\beta_2} \\ \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t+\epsilon}}·\hat{m}_t$$

    超参数建议值：$ \beta_1=0.9，\beta_2=0.999，\epsilon=10^{-8}$

特点：

1、相比于其他的自适应学习率优化算法，效果更好

参考文献

https://zhuanlan.zhihu.com/p/55150256

https://www.jianshu.com/p/0e561f62e64f